공분산

오늘 배운 공분산에 대해 복습하면서 더 공부하고,
부족한 부분을 채우기 위해 더 필요한 부분이 무엇인지 알아보자.

그 다음으로 수식을 Python을 통해 구현해볼 것이다.
마지막으로 numpy의 공분산 내장 메서드를 알아볼 것이다.

---

주관적으로 이해한 공분산이란,

두 데이터 집단의 상관 정도를 나타내는 지표. 방향성(비례, 반비례)은 제시할 수 있으나, 강도(얼마나 강력하게 관계를 가지는가)는 판단할 수 없다. 따라서, 공분산이 양수인지, 음수인지에만 초점을 맞춰서 판단해야 한다.

정도가 되겠다.

 

 

 

공분산을 구하는 수식을 알아보자.

공분산을 구하는 수식

하나 씩 잘라서 확인해보자.

 

가장 안쪽의

x의 편차를 구하는 수식

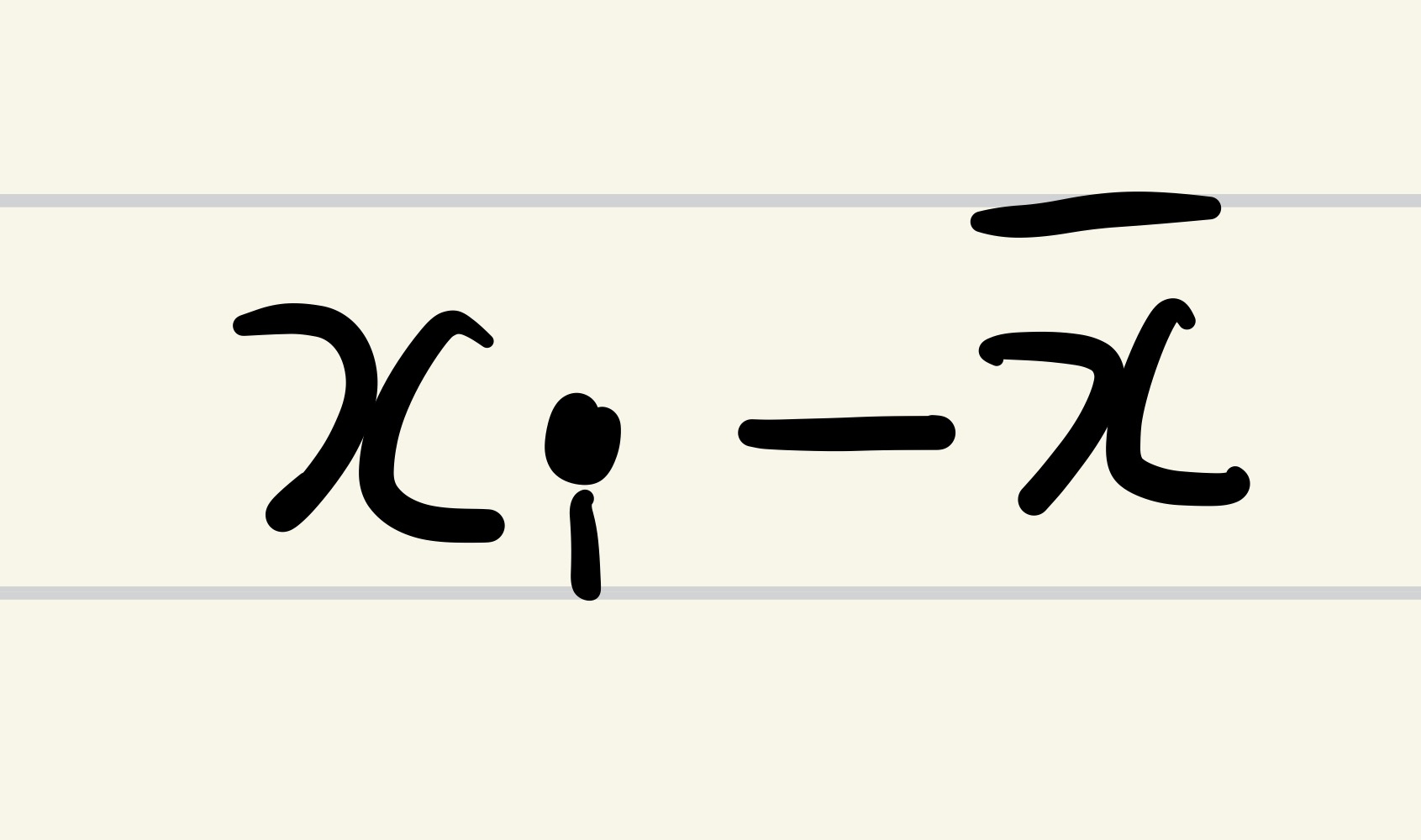
x의 편차를 구하는 수식이 보인다.
편차에 대해서는 분산, 표준편차를 공부하며 알아보았다.
편차는 관측값(데이터)와 평균값의 차이다.

 

그리고 그 옆의

y의 편차를 구하는 수식

y의 편차를 구하는 수식이 보인다.

 

그리고 이 각 편차를 곱해준다.

x의 편차와 y의 편차의 곱

이 것은 무엇을 의미할까.

동일한 지점에서의
x 데이터의 값의 편차와, y 데이터의 값의 편차를 곱하여
해당 지점의 상관 정도를 계산해내려는 의도인 것같다.

 

다음으로는 한 지점 지점마다의 두 편차의 곱을 모두 더한다.

시그마를 통해 x의 편차와 y의 편차의 곱를 모두 더한다.

 

마지막으로 전체 데이터 개수로 나누어준다.
공분산도 무언가의 평균이다.

전체 데이터 개수로 나누어 준다.

+ 공분산이란 동일한 지점의 x와 y의 상관 정도를 가지고,
x가 변화했을 경우, y가 어떻게 변화할지를 예측하는 지표라고 한다.

즉, 과거 ~ 지금의 x와 y를 가지고 미래의 x가 변할 때,
y의 값은 어떻게 될 것인가. 를 판단하기 위하여,

각 지점(과거 ~ 지금)마다의 편차들의 곱을 통해 
각 지점마다의 상관 정도를 구하고,

그 상관 정도들의 평균을 구하여,
전체적으로 두 데이터 집단의 관계(방향성)을 판단하는 것 같다.

 

이렇게 구해진 공분산 값이

양수라면, 양의 상관 관계로.
(x가 증가한다면, y도 증가한다.)
(y가 증가한다면, x도 증가한다.)

음수라면, 음의 상관 관계로.
(x가 증가한다면, y는 감소한다.)
(y가 증가한다면, x는 감소한다.)

판단한다.

 

 

 

후. 다시 Python으로 힐링을 해보자.
공분산 수식을 구현해 보자.

def covariance(x, y):
    cov = 0

    # x의 평균값을 구한다.
    x_ = sum(x) / len(x)

    # y의 평균값을 구한다.
    y_ = sum(y) / len(y)

    for xi, yi in zip(x, y):
        # x의 편차, y의 편차를 계산하여 곱한 후,
        # cov 에 모두 더한다.
        cov += (xi - x_) * (yi - y_)

    # 마지막으로 전체 데이터 개수로 나누어준다.
    return cov / len(x)


data1 = [80, 85, 100, 90, 95]
data2 = [70, 80, 100, 95, 95]
data3 = [100, 90, 70, 90, 80]

print(f'data1과 data2의 공분산 값 : {covariance(data1, data2)}')
print(f'data1과 data3의 공분산 값 : {covariance(data1, data3)}')

출력 결과 :

data1과 data2의 공분산 값 : 75.0
data1과 data3의 공분산 값 : -70.0

 

numpy의 공분산 내장 함수, cov를 이용하면,

import numpy as np


data1 = [80, 85, 100, 90, 95]
data2 = [70, 80, 100, 95, 95]
data3 = [100, 90, 70, 90, 80]

# np.cov 는 x의 분산, y의 분산을 함께 계산하여 돌려준다.
# 공분산만을 보기 위해 [0, 1] 를 붙여 사용하였다.
print(f'data1과 data2의 공분산 값 : {np.cov(data1, data2)[0, 1]}')
print(f'data1과 data3의 공분산 값 : {np.cov(data1, data3)[0, 1]}')

 

출력 결과 :

data1과 data2의 공분산 값 : 93.75
data1과 data3의 공분산 값 : -87.5

흠. 직접 구현한 공분산과 numpy의 공분산의 결과가 다르다.
그 이유는, numpy의 공분산에는 자유도가 적용되어 있기 때문이다.

 

 

 

그렇다면, 자유도는 무엇인가.

주관적으로 이해한 자유도란,

하나의 데이터에 2개 이상의 선택의 자유를 보장하기 위한 보정 장치. 색상이 여러개인 n개의 아이폰이 있고, n명의 사람이 순서대로 아이폰을 가져간다고 하면, 마지막 사람은 마지막 남은 아이폰을 가져가는 것이 확정된다. 이러한 확정 데이터는 통계, 분석에서는 예측 정확성을 떨어뜨리기 때문에, 아이폰의 개수보다 아이폰을 가져가려는 사람의 수를 줄이는 방법으로 확정 데이터를 없애려는 의도인 것 같다.

정도가 되겠다.

정확한 내용은 더 공부해야 알 것 같다. 허허.
알고리즘을 더 빠르게 끝내야 하겠다.

따라서 numpy의 공분산 내장 함수 cov와 같은 값을 보려면,

def covariance(x, y):
    cov = 0

    # x의 평균값을 구한다.
    x_ = sum(x) / len(x)

    # y의 평균값을 구한다.
    y_ = sum(y) / len(y)

    for xi, yi in zip(x, y):
        # x의 편차, y의 편차를 계산하여 곱한 후,
        # cov 에 모두 더한다.
        cov += (xi - x_) * (yi - y_)

    # 마지막으로 전체 데이터 개수 - 1로 나누어준다.
    return cov / (len(x) - 1)


data1 = [80, 85, 100, 90, 95]
data2 = [70, 80, 100, 95, 95]
data3 = [100, 90, 70, 90, 80]

print(f'data1과 data2의 공분산 값 : {covariance(data1, data2)}')
print(f'data1과 data3의 공분산 값 : {covariance(data1, data3)}')

출력 결과 :

data1과 data2의 공분산 값 : 93.75
data1과 data3의 공분산 값 : -87.5

 

어렵다. 어려워. 흠.
하지만 나를 죽이지 못하는 지식은, 나를 더 강하게 할 뿐. ㅋ.ㅋ